Nahom Derese

April 10, 2023 at 9:03:00 PM

Trigonometric identities

Trigonometric identities are mathematical equations involving trigonometric functions (such as sine, cosine, tangent, cotangent, secant, and cosecant) that hold true for all values of the variables within their respective domains. Trigonometric identities are widely used in mathematics, physics, and engineering to simplify and manipulate trigonometric expressions and solve trigonometric equations.

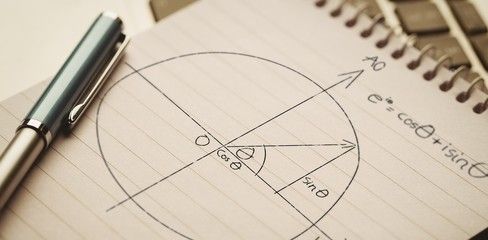
Here are some common trigonometric identities: Trig.jpg

Pythagorean Identities

sin2(x)+cos2(x)=1sin^2(x) + cos^2(x) = 1
tan2(x)+1=sec2(x)tan^2(x) + 1 = sec^2(x)
cot2(x)+1=csc2(x)cot^2(x) + 1 = csc^2(x)

Reciprocal Identities

csc(x)=1/sin(x)csc(x) = 1/sin(x)
sec(x)=1/cos(x)sec(x) = 1/cos(x)
cot(x)=1/tan(x)cot(x) = 1/tan(x)

Quotient Identities

tan(x)=sin(x)/cos(x)tan(x) = sin(x)/cos(x)
cot(x)=cos(x)/sin(x)cot(x) = cos(x)/sin(x)

Co-function Identities:

sin(pi/2−x)=cos(x)sin(pi/2 - x) = cos(x)
cos(pi/2−x)=sin(x)cos(pi/2 - x) = sin(x)
tan(pi/2−x)=cot(x)tan(pi/2 - x) = cot(x)
csc(pi/2−x)=sec(x)csc(pi/2 - x) = sec(x)
sec(pi/2−x)=csc(x)sec(pi/2 - x) = csc(x)
cot(pi/2−x)=tan(x)cot(pi/2 - x) = tan(x)

Double Angle Identities

sin(2x)=2sin(x)cos(x)sin(2x) = 2sin(x)cos(x)
cos(2x)=cos2(x)−sin2(x)=2cos2(x)−1=1−2sin2(x)cos(2x) = cos^2(x) - sin^2(x) = 2cos^2(x) - 1 = 1 - 2sin^2(x)
tan(2x)=(2tan(x))/(1−tan2(x))tan(2x) = (2tan(x))/(1 - tan^2(x))

Sum and Difference Identities

sin(x+y)=sin(x)cos(y)+cos(x)sin(y)sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
cos(x+y)=cos(x)cos(y)−sin(x)sin(y)cos(x + y) = cos(x)cos(y) - sin(x)sin(y)
tan(x+y)=(tan(x)+tan(y))/(1−tan(x)tan(y))tan(x + y) = (tan(x) + tan(y))/(1 - tan(x)tan(y))
sin(x−y)=sin(x)cos(y)−cos(x)sin(y)sin(x - y) = sin(x)cos(y) - cos(x)sin(y)
cos(x−y)=cos(x)cos(y)+sin(x)sin(y)cos(x - y) = cos(x)cos(y) + sin(x)sin(y)
tan(x−y)=(tan(x)−tan(y))/(1+tan(x)tan(y))tan(x - y) = (tan(x) - tan(y))/(1 + tan(x)tan(y))

These are just some of the many trigonometric identities that are used in mathematics. Familiarizing yourself with these identities and understanding how to apply them can be helpful in solving trigonometric equations, simplifying trigonometric expressions, and analyzing trigonometric functions.